Economics 100A
Prof. Yang

Solutions to Homework Problems                     Chapter:  1  2  3  4  5   6  7  8  9

Chapter 6

Numerical

1. a)     Y = C+I+G+X

= a+b(1 - t)Y+I+G+(g - mY)

                   = (a+ I+ G + g)/[1 - b(1-t) + m] = 2820/.47 = 6000.

The multiplier is now equal to 1/0.47 = 2.13, which is smaller than the value of the multiplier obtained on page 165 of the text.

b) Y_d = (1 - t)Y = .7 x 6000 = 4200,

C = a + bY_d = 220 + .9 x 4200 = 4000,

S_p= Yd - C = 4200 - 4000 = 200,

T = tY = .3 x 6000 = 1800,

S_g =T - G = 1800 - 1200 = 600,

X = g - mY = 500 - .1 x 6000 = -100, and so

S_r = -X = 100.

Therefore 900 = 200 + 600 + 100; that is, I =S_p + S_g + S_r, and S_p = 200/900 = 22.2% of I, S_g = 66.7% of I, and Sr = 11.1% of I.

c) If I increases by $100, then

                    D I = 100,

                    D Y = 1/.47 = 213,

                    D Y_d = .7D Y = 149,

            and   D C = .9D Y_d = 134;

            thus  D S_p = D Y_d - D C = 149 - 134 = 15.

                    D T = .3D Y = .3(213) = 64;

            thus D S_g = D T - D G = 64 - 0 = 64

        and   D S_f = -D X = -(D g - mD Y) = -[0 - (.1)213] = 21.

Note again that 15 + 64 + 21 = 100; that is

                    D S_p + D S_g + D S_f = D I.

 2.        Y = 160 + .8(.75Y-200) + 200 + 200 = 400 + .6Y

         .4Y = 400

            Y = 1000.

a) T = .25Y + 200 = 450.

        S_g =T - G = 250.

b) Y = 480 + .6Y = 1200.

Lump sum tax multiplier = D YID Z = 200/-100 = -2.

T = .25(1200) + 100 = 400.

S_g = 200.

c) Decrease in tax receipts is only 50, instead of the full 100, because the expansion in output increases the amount of receipts from the income tax.

d) No, it cannot. The change in tax receipts that results from the change in lump sum taxes is given by

             D T = tD Y + D Z

= t(a D Z) + D Z

where a is the lump sum tax multiplier, which must equal -b/[1 - b(1 - t)] where b is the MPC. Thus,

 

 

 

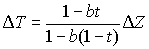
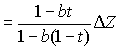
Since the fraction must be positive, we know that D T and D Z have the same sign. Thus, a tax cut
(D Z < 0) must decrease tax revenue (D T < 0) so long as 0 < b and t< 1. The spending balance model ignores the possibility that tax policy can affect labor supply and; thus potential GDP. Supply siders would object to this omission.

Analytical

1. a) You must forecast values for the exogenous variables I and G. Given I and G, the model can be solved for equilibrium values of C, X, and Y.

b) No. In such an economy output is determined by plan, not by aggregate demand. In fact, in such an economy, demand would be determined by output, where output is exogenous.

3. a) S_P= -a+(I-b)Y_d.

b) With no investment or foreign saving, private saving plus government saving sum to zero, or private saving must equal the government budget deficit.

c)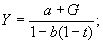

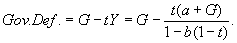
The expressions are the same.

 

4. a) Equilibrium income is given by Y = (a - bT + 1 + G)/(1 - b). The tax multiplier is thus -b/(1 - b).

b) The government spending multiplier is equal to 1/(1 - b), which exceeds the tax multiplier in magnitude since b < 1.

c) Y will change by the amount of increase (or decrease) in government spending and taxes. The sum of the government spending multiplier is known as the balanced budget multiplier and equals 1 in this model.

---

Back to Prof. Yang's Homepage