Section IV:

I. Correlation & Regression (looking for relationships between variables)

• Correlation:

  
  
  
  
  

  • e.g.

    
    
    
    

• Regression:

  
  
  
  
  

  • e.g.

    
    
    
    

• Correlation & Regression are closely related

   

  •  

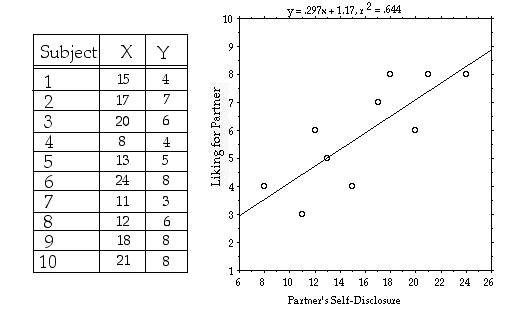
Sample Data:

• In a study on relationships, a researcher was interested in the relationship between amount of partner's self-disclosure and liking for the partner.

• Correlation:

  
  
  
  
  
  
  

• Regression:

  
  
  

  
  

Scatterplot

II. Overview of Correlation (r)

• Pearson Correlation
  
  • 
    
    
    
    
    
    
    
    
  • "r" is Pearson correlation coefficient
    
    • 
      
      
    • 2 characteristics that define r
      
      • Direction:
        
        • if positive

          
          
          

           

          e.g.
          
          
          
          
          

        • if negative

          
          
          
          
          e.g.
          
          
          
          
          

  • Magnitude:
    
    • 
      
      
      
      
    •  

e.g.

• r = ______ or ______ if all points lie on regression line

• examples:

III. Inferences about Correlation

• draw inference about population parameter r, (rho) from sample statistic, r
  
• r is ________________ for r
  
• to draw inferences we need a sampling distribution of the sample statistic
  
  
  • use new sampling distribution, r distribution
    
    
• can answer both correlation & regression questions by determining whether the correlation is significantly different from zero.
  
  • if corr = 0

    
    
    

  • if corr 0

    
    
    

Hypothesis Testing Steps:

1. State Hypotheses

• H_A:
  
  
  
• H₀:
  
  
  
• ex: (partners)
  
  
  
  

2. Make Graph

3. Find Critical Value (a = .05) New Table

• need a, df (n-2), and directionality
  
  
• ex: (partners)
  
  
• r_crit =

4. State Decision Rules

• ex:
  
  • 
    
    
    
    
    
  •  

5. Calculate Test Statistic

• Calculating r

• SSxy =

  
  
  
  
  
  

• SSxx =

  
  
  
  
  
  

• SSyy =

  
  
  
  
  

   

• Calculations (partner example)

Sxy =

Sx =

Sy =

Sx2 =

Sy2 =

 

• SS_xy =

  
  
  
  
  
  

• SS_xx =

  
  
  
  
  
  

• SS_yy =

  
  
  
  
  
  

• r_calc =

6. State Assumptions

• subjects are randomly and independently sampled
  

• population distributions of X & Y are normal

 

 

7. Draw Conclusion (include both magnitude and direction in conclusion)

• ex:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Coefficient of Determination (r²)

• 
  
  
  
  
  
  
  
  
  
  
  
• partner ex: r = .80, so r² =

   

• 
  
  
  
  
  
• ex: correlation between severity of childhood sexual abuse and severity of psychiatric problems as an adult: __________
  

• r² =

  
  

• interpretation:
  

• Practice: Test the hypothesis that # of cigarettes smoked daily is positively correlated with # of days absent from work.

 

Subject	# cigarettes	days absent
1	0	1
2	0	3
3	0	8
4	10	10
5	13	4
6	20	14
7	27	5
8	35	6
9	35	12
10	44	16
11	53	10
12	60	16

• Hypotheses

 

 

• Graph

• Critical Value, r_crit (a = .01)

  
  

• Decision Rule

  
  
  
  

• Test Statistic
  • SS_xy = 792.25
  • SS_xx = 4842.25
  • SS_yy = 284.25
    
    
    
    
    
    
• Conclusion

  
  
  

• p-value, Type I & Type II errors

  
  

  
  
  
  

• r² value & interpretation

IV. Caveats to Correlation Analysis

• Correlation does not imply causation
  
  
  • a significant correlation may occur for 3 (or more) reasons:
    
    
    • 
      
      
      
      
    • 
      
      
      
      
    • 
      
      
      
      
      
      
      
      
  • ex: Ice cream sales (X) and crime rate (Y) in NYC correlate about __________
    
    • 
      
      
      
    • 
      
      
      
      
      
      
      
      
      
      
  • ex: Marital Satisfaction (X) and Incidence of marital violence (Y) correlate about _________
    
    • 
      
      
      
    • 
      
      
      
      
      
      
      
      
      
• Outlier Problems
  
  • outliers

     

  • can have big impact on r_calc

    
    

  • Solution:

• Difficulties Combining Groups' Data
  
  
  • can be problematic if calculating a correlation across several groups' data

    
    
    

  • ex: correlation of mental age with fear of dying
    
    
    • 1st graders:
      
      
      
    • 6th graders:
      
      
      
    • Combined:
      
      
      
  • 
    
    

• Nonlinear Relationships
  
  • r_calc may be small
    
    
    
  • 
    
    
    
  • 
    
    
    
  • ex: correlation between anxiety and performance

• Restricted Range