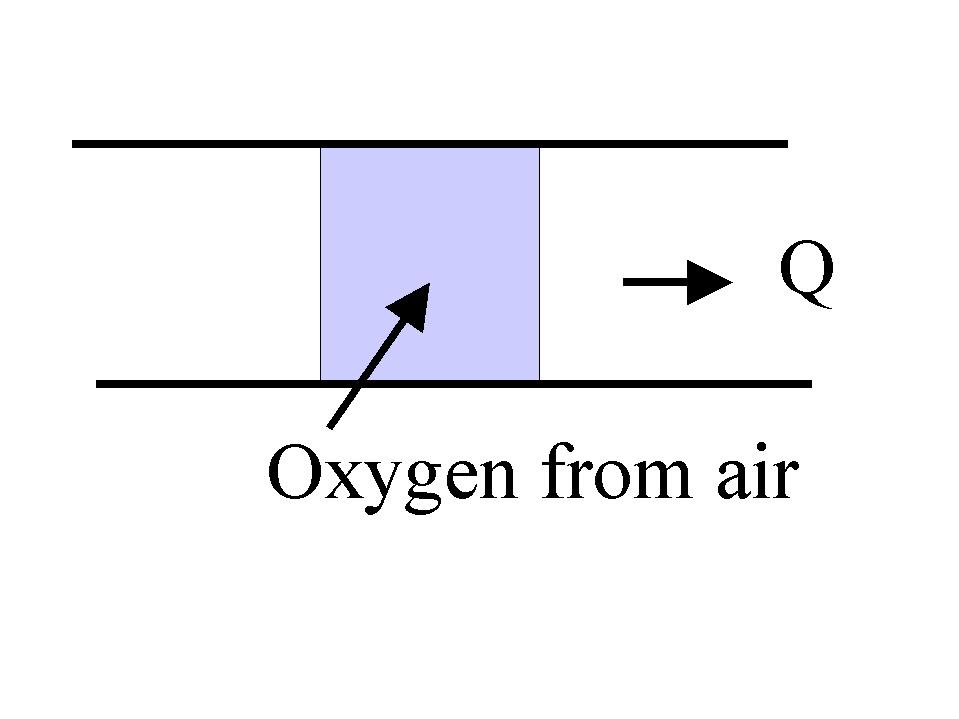
Derivation of the Dissolved Oxygen Sag Equation
Consider an element of water in a stream. We will track the element as it moves downstream with the general flow of water.

Setting up the differential equation
The mass balance equation written out in words is:
Accumulation = In - Out + Reaction
Because we are looking at the element by itself, there is no flow of water into or out of it. So the mass balance on oxygen becomes:

Let's look at these two rates. The rate of O2 removal by biodegradation is:
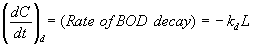
where
L = ultimate BOD of organics remaining in the water at any time t
kd = first-order degradation rate constant. kd is related to, but is not numerically the same as, kBOD, the rate constant in the BOD test.
The rate of O2 transfer from the atmosphere (called reaeration) is:
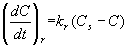
where
C = dissolved oxygen concentration (DO)
Cs = dissolved oxygen concentration at saturation, predicted from Henry's Law
kr = reaeration rate constant. This value will be related to the characteristics of the stream.
Note that this is the same form of equation we used in the gas transfer lab. Now, substitute the rate expressions into the mass balance.
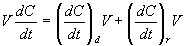
![]()
Mathematically, it is convenient to express everything in terms of the deficit, D.
D = (Cs - C)
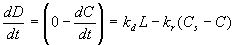
This is the basic differential equation that must be solved.
Solving the differential equation
Solving the differential equation requires the use of integrating factors. First substitute the BOD decay equation for L.
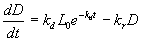
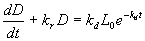
This arrangement matches the standard form:
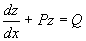
So, use the integrating factor:
![]()
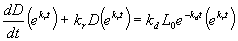
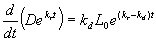
Separate variables and integrate.
![]()

Apply the boundary condition that at t = 0, D = D0
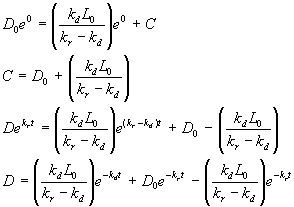
Finally, after grouping like terms, the integrated equation is:
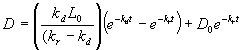
where
L0 = ultimate BOD in the water at t = 0
D0 = deficit at t = 0.
Note that both L0 and D0 are the values in the stream after any external waste streams have been mixed in.
This equation is known as the DO sag equation (for its distinctive shape) or the Streeter-Phelps equation, after the gentlemen who first published it in 1925.
Using the DO Sag equation
Of course, the fish aren't interested in the deficit. They want to know the concentration. This can be calculated from:
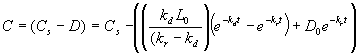
When this equation is plotting this equation with typical values, the following curve is generated:

We can use the DO sag equation to find the concentration at any point downstream of a waste discharge as long as we know the travel time to that point, which is easy to calculate if the stream velocity is known.
To protect fish, engineers often want to know the minimum oxygen concentration that can be expected as a result of a waste discharge. This is called the critical point (critical from the point of view of the fish). The travel time to the lowest point in the sag is the critical time. Using the critical time (tc), we can easily calculate the critical deficit (Dc), and the minimum DO concentration.
To find the critical time and deficit, differentiate the Streeter-Phelps equation and set it equal to zero.

If you divide through by ![]() , bring the right hand term to the other side of the equal sign, take the natural log of both sides, and solve for t = tc, you get:
, bring the right hand term to the other side of the equal sign, take the natural log of both sides, and solve for t = tc, you get:
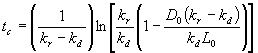
To solve for the critical deficit, Dc, you could plug this expression for tc into the Streeter-Phelps equation, but that would give you a massive algebra headache. It's easier to realize that at the bottom of the sag, dD/dt = 0. This allows us to go back to the differential equation.
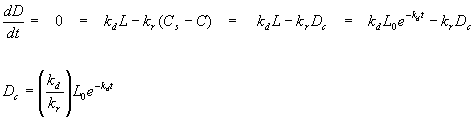
![]()
Now, the minimum concentration Cmin can be calculated from
Cmin = Cs - Dc
Note that tc and Dc are single values at a specific location. If we want the DO at any other location, we would use the Streeter-Phelps equation itself.