Confidence Intervals
| Confidence Interval for a Population Mean |
| Confidence Interval for a Population Proportion |
| Confidence Interval for a Population Variance |
| Confidence Interval for Difference of Proportions |
-
Point Estimators and Confidence Intervals
-
Point Estimators
Suppose that you are asked to determine the mean (i.e. average) age of CSUS students during the current semester. The population, all CSUS students consists of approximately 20,000 individuals. To obtain the age of every student would be time consuming and costly. However, you could estimate the mean age by taking a small random sample of current students, get the age of each sampled student, and average these numbers. For example, a random sample of 10 students might produce the following collection of ages: 19, 21, 30, 32, 22, 23, 26, 18, 20, and 21. The average of these numbers, 23.2 is an estimate of the mean age of all students. A single number estimate is called a point estimate.
There are a couple of questions connected with this point estimate. First, is the mean of the sample the best point estimate of the population mean. Perhaps there are ways, other than averaging, to combine the sampled ages to produce a better estimate of the population mean. Statisticians have developed some measures of quality for point estimators. One of them is called 'unbiasedness.' An estimator of a population parameter if when all possible samples are selected from the population and the estimator is computed for each sample, the average of these estimators equals the population parameter that you are trying to determine. In statistical terms, and unbiased estimator is an estimator whose expected value equals the population parameter. In symbols, an estimator of a parameter
of a population is denoted by 
(read 'theta hat'). An unbiased estimator satisfies the
condition 
.
It can be shown that the sample mean is an unbiased estimator of the
population mean.Estimators of population parameters vary from sample to sample. So, a second desirable property of a point estimator is that these estimators have minimal variation, that is, minimal variance. It turns out that among all unbiased estimators of the population mean for a sample of fixed size n, the sample mean has the smallest variance. So, given the 10 data values, the average of them, 23.2, is the best point estimator of the population mean age of CSUS students in the sense that it is unbiased and has the smallest variance.
In summary, a point estimate of a population parameter is a single number based on the sample used to estimate a population parameter.
-
Confidence Intervals
Given a single number point estimate of a population parameter like the point estimate 23.2 for the mean age of all CSUS students, you might wonder how close this number is to the population mean. It is unlikely that the estimate, 23.2, is exactly equal to the population mean. If it isn't equal, is it off by 0.2 years? by 1 year? by 10 years? If you are only given the single number estimate, you have no information concerning the 'closeness' of the estimate to the parameter. Confidence intervals are numerical intervals in which the population mean might lie. Together with the interval, a measure of certainty that the parameter lies within the interval is given. For example, in the example of the mean age of CSUS students, a confidence interval would be given in the following form: 'you are 95% confident that the mean age of CSUS students lies in the interval from 21.2 years to 25.2 years.' These two items, the confidence level, and the length of the confidence interval give you much more information than a single number.
In the following sections the meaning of the term confidence level, and the processes used to compute the endpoints of confidence intervals are shown for several population parameters.
To Top
-
-
Confidence Interval for a Population Mean
-
Population Standard Deviation Known
In this section a confidence interval for the population mean when the population standard deviation is know is developed. You might ask, why if the population mean is unknown, would the population standard deviation be known? In many cases the population standard deviation is unknown, and confidence intervals will be developed for that situation later. Also, in many situations you may not know the population mean but you do know the population standard deviation. These are the situations that are considered here.
From your work with the sampling distribution of sample means, you know that the sampling distribution of sample means is approximately normal, its mean is the mean of the population from which samples are selected, and its standard deviation is the population standard deviation divided by the square root of the sample size. If a random sample of size n is selected and the mean computed, the following statement is true:
A confidence interval with confidence level (1-
)100% is
determined as follows: (1) find two z-values with the property that between
them the probability is 1-. By symmetry of the normal density
function, one of the z-values will be the negative of the other
z-value. (2) Put each of these z-values in the formula shown above and
solve the equation for 
.
(3) The interval formed by these two solutions is the 1-alpha confidence
interval for .
The formula for the confidence interval can be written
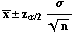
where
is
the z-value with probability 
to
the right of it.
When a confidence interval based on a single sample is computed, this confidence interval might or might not contain the population mean. If the confidence interval contains the mean, it is called 'good', and if the confidence interval doesn't contain the mean, it is called 'bad.' Since, in practice, you won't know the population mean, you won't know whether the single confidence interval that you compute is 'good' or 'bad'. However, the following demonstration shows that in the long run (1-
)100%
of the confidence intervals will be good. A
link to a Hyperstat Online page from Rice University that
demonstrates the meaning of confidence level is found here.
-
Population Standard Deviation Unknown
To find a (1-
)100%
confidence interval for
when the population standard deviation is unknown, you would like to replace
with s, the
sample standard deviation in the formula 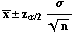However, if you replace
with s, 
doesn't have a standard normal distribution. If it did, we could find two z-values such that the probability between them is (1-
), put each of
them on the left side of the last expression, and solve for ,
thus producing the desired confidence interval. As you take all possible random samples for size n from a population, what kind of probability distribution does
have?
For a general population and small sample size (n<30), there is no
answer. If n is 30 or more the distribution is close to a standard
normal distribution, but for n<30, the only case in which the probability
distribution is known is the case in which the population from which samples
are selected is normally distributed. In that case the statistician
Gossett described the probability distribution as a 'Student's
t-distribution with n-1 degrees of freedom'. What is the Student's
t-distribution with n-1 degrees of freedom? The following graph shows
a standard normal distribution in black, a t-distribution with 5 degrees of
freedom in blue, and a 5-distribution with 20 degrees of freedom in red.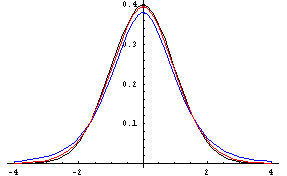
You can see that the t-distributions have slightly greater variability than the standard normal distribution. Also, as degrees of freedom increase, the t-distribution curve gets closer to the standard normal curve. You can use the following page to find any t-distribution probabilities. Link to a calculator page from the UCLA Statistics Department that will allow you to find the cdf (or pdf) for any Student's t distribution (Called the Student Distribution).
A formula for a (1-
)100%
confidence interval for
when is unknown
is -
where t has n-1 degrees of freedom.
To Top
-
Confidence Interval for a Population Proportion
Confidence intervals for population proportions appear almost daily in newspapers, in magazine articles, and on radio and television broadcasts. They are used to predict the proportion of a population with a certain characteristic. For example, the proportion of a population with brown hair, the proportion of a population favoring the death penalty, the proportion of the population that smokes, etc. A most interesting application of confidence intervals is prediction of election outcomes. Professor Richard Lowry of Vassar College has written a wonderful web page on election polling and the 2000 presidential election. The proportion of the population possessing the characteristic of interest is denoted by p. Since the population is often very large, in order to predict p, a random sample of size n is selected from the population. If X is the number of elements of the sample with the characteristic of interest, X can, in most cases, be considered to be a binomial random variable with parameters n and p. The sample proportion with the characteristic of interest is denoted by
.
Then =X/n.
Since
is an average, the central limit theorem implies that for large n, approximately
normally distributed with mean E[X/n]=(1/n)E[X]=(1/n)(np)=p and Var[X/n]=(1/n2)Var[X]=(1/n2)(npq)=pq/n.
This means 
has a normal distribution. To find a (1-
)100%
confidence level confidence interval find the appropriate z-values, put
them in the last equation, and solve for p. You will get
There is a problem with this expression. Since you are finding a confidence interval for p, you don't have a value for p. This problem can be overcome by using the estimator
in
place of the unknown p. This results in the following confidence
interval formula
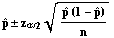
To Top
-
Confidence Interval for a Population Variance
A (1-
)100%
confidence level confidence interval for the population variance,2,
can only be found when the population from which the sample is drawn is normally
distributed. In this case, you have seen that the quantity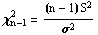
has a Chi-Square distribution with n-1 degrees of freedom where S2 is the sample variance computed by using the formula
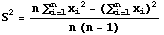
To find the confidence interval, use the table of the Chi-Square distribution with n-1 degrees of freedom to find two Chi-Square values such that the probability between them is 1-
.
These two values are denoted by 
and 
. By
replacing the left hand side of the expression for Chi-Square shown above by
each of these quantities and solving in each case for 2
you get the confidence interval from 
to
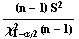
To find a confidence interval for
simply
take the square root of the endpoints of the confidence interval for the
variance.
To Top
-
Confidence Interval for Difference of Proportions
To Top