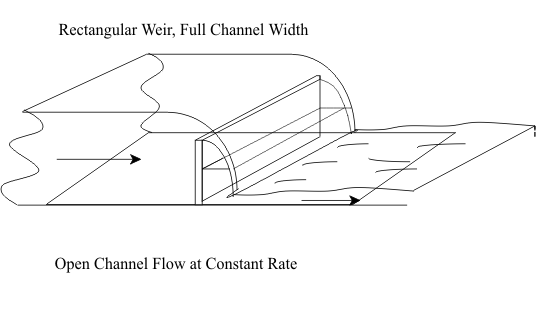
Basic Weir Theory

Weirs measure flows in open channels

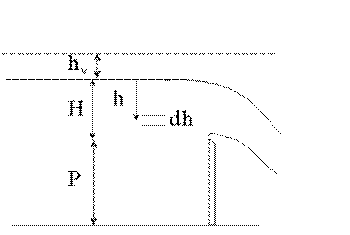
       Bernoulli equation for ideal flow: (q = flow per unit width)

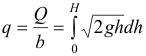
       Energy Equation: (H_T = total head)

          H_T = H + h_v = H + v²/2g

Flow Parameters

             H_T = H + v²/2g 

                  v = (2g(H_T - H))^0.5

               v = (2g H (H_T/H - 1))^0.5

                = C (2g H)^0.5

         Flow  Q = vA = C (2g H)^0.5 A

       Weirs may be broad-crested or sharp-crested

       The ones we use in our lab are sharp-crested

Sharp-Crested Weirs

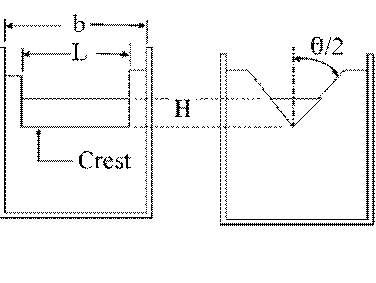
             Rectangular: A = L H 

             V-notch: A = H^2.5 tan(θ/2)

       Weir Equations

                                    Q = vA

             Rectangular Weir: Q = C (2gH)^0.5 L H

                C= arbitrary constant

                                    Q = C (2g)^0.5 L H^1.5

                                    = C L H^1.5 or C H^1.5

             V-notch Weir: Q = C (2g H)^0.5 H² tan(θ/2)

                                    = C H^2.5 tan(θ/2) or C H^2.5

                 For θ = 90° V-notch, C ≈ 2.5, so approximately

                                           Q = 2.5 H^2.5

FOR OUR EQUIPMENT

              Rectangular weir has L = b, where

                                    b is channel width

                     Thus, Q = C  L H^1.5

              V-notch weir has

                              Q = a H^b tan (θ/2)

              Our θ = 90°, so our value should be near

                            Q = 2.5 H^2.5

Flow Over Sharp-Crested Weir

V-notch or Triangular Weir

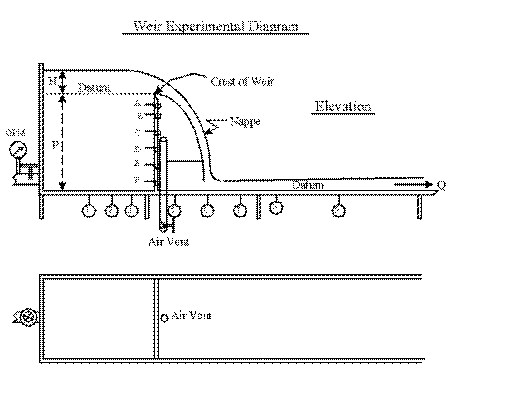
Experimental Set-Up

      (See diagram on next view graph)

Water Surface Profile In Rectangular Channel With Weir

      Taps 1-3 before weir; tap 5+ after weir

      Skip tap 4 (under weir)

      Two levels between taps 4 & 6

            Over-flow of weir not in manometer taps

            Point gage can hit both areas

            (Sketch the pattern; points vary too much to just use data points)

      Supercritical flow after weir

      Go far enough to see smooth surface

Weir In Half-Meter Flume In CE Lab

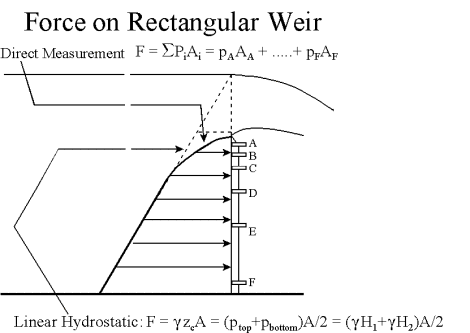
Direct Measurement:

      F = Σγb(z_w-z₀+y_ti)Δy_i

Hydrostatic Force:

      F = γb((z_w-z₀)²-((z_w-z₀+y_w)²)/2