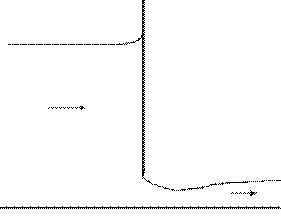
SLUICE GATE THEORY

Open Channel Flow

            Pressure at water surface is atmospheric

or zero gage pressure

            Water surface = piezometric head level

I.e., level registered by manometer with a piezometric tap

Open channel flow in general, has two possible flow depths for each energy level

              Subcritical and supercritical

       Sluice gate changes flow from

               subcritical to

               supercritical

FLOW UNDER SLUICE GATE

Like Flow Through Orifice

       Minimum cross-sectional area (vena contracta)

              slightly downstream from the gate

Ideal Flow Theory (No Energy Losses)

       Q = V₁*A₁ = V₂*A₂

Experimental Studies

       Discharge coefficient

              Flow is never really “ideal”

              Coefficient is related to relative size of gate

                     opening

Brater & King summarize some of these

              General form Q = C*A*(2g*dH)^0.5

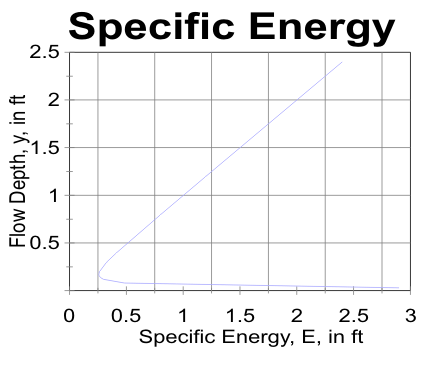
SPECIFIC ENERGY

Energy in an open channel measured relative to the

              channel bottom    E = y + V^2/2g

For two values of y with the same value of E

E = y₁ + V1^2 /2g = y₂ + V₂^2 /2g

Combine this with the continuity equation,

              V₁*b*y₁ = V₂*b*y₂

Now we can eliminate one of the velocities and compute

the other velocity without using Q.

This gives some experimental data for a two-dimensional

              plot of specific energy to compare with the

              theoretical equation

SPECIFIC ENERGY PLOT

To use this, we measure y₂ at the vena contracta.

As an aside, the specific energy function,

               E = y + Q^2 /2g*b^2 y^2,       is actually cubic in y

                I.e.,        -y^3 + E*y^2 = Q^2 /2g b^2

       The subcritical and supercritical flows are two of the

              three areas for the solution. The third area of the

              solution has a negative value of y, which is

              meaningless for open channel flow

SLUICE GATE EXPERIMENT

Study the application of one-dimensional flow analysis involving continuity, energy and momentum equations to a sluice gate in a rectangular channel

Flow Under A Sluice Gate

Two flow depths, subcritical and supercritical, for each energy level

Compare the measured values of y₂ with values computed

     for observed y₁

Note: Manometer (pressure) taps show the water pressure on the other side of the sluice gate in the center of the channel

FORCE BY MOMENTUM EQUATION

F_x = G* V_x *Q (with G=gamma) gives

                       F_g = G*[Q*(V₁ -V₂) + 0.5*b* (y₁^2-y₂^2)]

where G = density of water

       g (in the drawing) = specific weight of water

       Q = flow rate

       v₁, y₁ = upstream velocity and depth

       v₂, y₂ = downstream velocity and depth

       b = width of rectangular channel

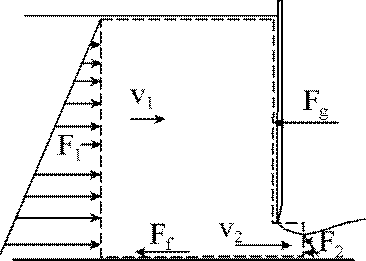
Force By Direct Measurement & By Hydrostatic Model

Direct measurement uses pressure measured at several points along the gate. The key is to select the area you associate with each pressure value.

Linear hydrostatic pressure uses the simple triangular pattern of pressure, with the average pressure at the center point times the area. (In our experiment, the top pressure is atmospheric, which we use as H₁ of zero.)

Flow With An Abrupt Drop-Off

  First a little background

Flow Types:

Zones 1, 2, & 3: Above both normal & critical depths (1), between normal & critical (2), and below both normal & critical (3)




Mild, Critical, & Steep slopes: Whether normal depth is above, at, or bellow critical depth




Speed of Sound in Water




Message moves to inform upstream flow of what is going on down-stream




If flow is subcritical, message goes up-stream and down-stream so flow can adjust




If flow is supercritical, water is moving faster than the message, so no message goes up-stream

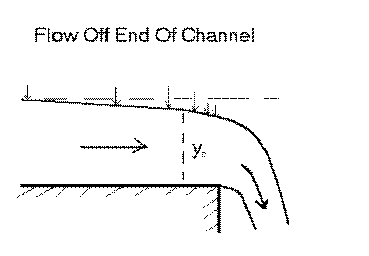
Flow Over The End of Our Horizontal Channel

Flow starts at subcritical because slope is zero & normal depth is infinitely high




Technically our flow is H2




Drop-off at end goes to critical depth and width becomes less as water drops (See graph below)




Zero pressure and Z1+V1^2 /2g = Z2+V2^2 /2g means Z is dropping & V is rising




(Water molecules grab each other, so those off the edge pull the ones behind to a little faster than speed of sound.)

SLUICE GATE EXPERIMENT: PREPARATION

OBJECTIVES (Presented above)

APPARATUS (Same flume & measurement taps as for

        Weir Experiment, except tap on the sluice gate)

PROCEDURE:

Set up experiment.

Open surge tank valve. Open both the head and the tail (sluice) gates of the half-meter open channel unit




Determine the longitudinal profile along the centerline of the floor of the flume to get point gage zeros. (If not clear from a prior experiment.)




Remove air from all manometric tubing. Locate the pressure taps in the gate and on the floor of the flume and match them to the manometer columns.




Close the drain valve, start the large pump, and open the intake valve.

SLUICE GATE EXPERIMENT: Data Collection

Measure the profile and the sluice gate variables.




Establish a steady flow in the flume




Lower the upstream sluice gate until it impinges on the flow.




Slowly lower the gate until the flume is nearly full. Wait for the flow to reach the steady state.

   [Note: remove air from the manometer tubes A-F.]




Record the flow depths of the water surfaces both upstream and downstream of the gate. For the supercritical section, you are trying to measure at the vena contracta.




Repeat step d until you have at least 6 measurements of depth





Measure the water surface profile near the downstream drop-off




Open both sluice gates to a level above the surface

    of the water.




Measure the depth of the water at enough points to

    show the surface shape. Note that the points need

    to be closer as you near the end of the channel.





Shut off the flow. Turn off the pump, close the intake

  valve, and open the drain valve on the head tank.

Sluice Gate in Our Flume

SLUICE GATE EXPERIMENT: RESULTS

Data, Calculations, and Results:

Attach your data sheet and sketch of the experimental set-up

 


Using the continuity equation between the upstream and downstream flows (latter at the vena contracta) compute the velocities on both sides of the gate for each pair of flow depths.
From Q = V_iA_i

              V₁ = Q/(b*y₁) and V₂ = Q/(b*y₂)

 

Compare the specific energy (E_i = y_i + V_i^2 /2g) plot for the observed depths and computed velocities with the theoretical plot at the same flow rate, Q

 

Compare the measured contraction coefficient with any hydraulic literature reference.

 




Using your depth measurements upstream of the gate and at the vena contracta, along with the continuity and energy equations, compute the flow rate and compare it with the rate given by the flow meter

               Q = V₁*A₁ = V₂*A₂

       E_i = y_i + V_i^2 /2g        or y₁ + V₁^2 /2g = y₂ + V₂^2 /2g

       Combining these: Q = 2g*b* y₁* y₂ / (y₁ + y₂)^0.5

 

Compute the force on the gate using (a) the measured pressures, (b) hydrostatic assumption, and (c) the momentum equation. Compare the three values in terms of accuracy and convenience.

 

Plot the pressure distributions on the upstream side of the sluice gate from the measured pressures and from the hydrostatic assumption on the same chart and compare the two patterns.

 

Plot the flow depth data for the flow off the end of the half-meter flume.