SLUICE GATE EXPERIMENT

Open Channel Flow

Pressure at water surface is atmospheric or zero gage pressure
Water surface = piezometric head level
    I.e., level registered by manometer with a piezometric tap
Open channel flow, in general, has two possible flow depths for each energy level: Subcritical and supercritical
       Sluice gate changes flow from
      subcritical     to     supercritical


FLOW UNDER SLUICE GATE


Like Flow Through Orifice
Minimum cross-sectional area (vena contracta) is slightly downstream from the gate

Ideal Flow Theory (No Energy Losses)
Q = V₁*A₁ = V₂*A₂

Experimental Studies
Discharge coefficient
Flow is never really “ideal”
Coefficient is related to relative size of gate opening

Brater & King summarize some of these
       General form Q = C*A*(2g*dH)^0.5




SPECIFIC ENERGY


Energy in an open channel measured relative to the channel bottom    E = y + V²/2g

For two values of y with the same value of E
E = y₁ + V₁² /2g = y₂ + V₂² /2g


Combine this with the continuity equation,
              V₁*b*y₁ = V₂*b*y₂
Now we can eliminate one of the velocities and compute the other velocity without using Q. This gives some experimental data for a two-dimensional plot of specific energy to compare with the theoretical equation

To use the specific energy plot, we measure y₂ at the vena contracta.
As an aside, the specific energy function,
E = y + Q² /2g*b² y²
is actually cubic in y
  I.e.,        -y³ + E*y² = Q² /2g b²
The subcritical and supercritical flows are two of the three areas for the solution. The third area of the solution has a negative value of y, which is meaningless for open channel flow

SLUICE GATE EXPERIMENT

Study the application of one-dimensional flow analysis involving continuity, energy and momentum equations to a sluice gate in a rectangular channel

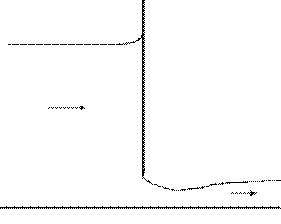
Flow Under A Sluice Gate
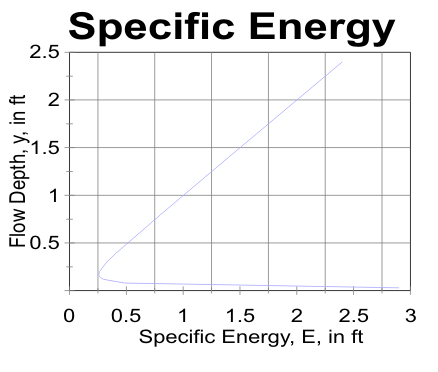
As stated earlier, there are two flow depths, subcritical and supercritical, for each energy level
The easiest approach is to compare the measured values of y₂ with values computed for observed y₁


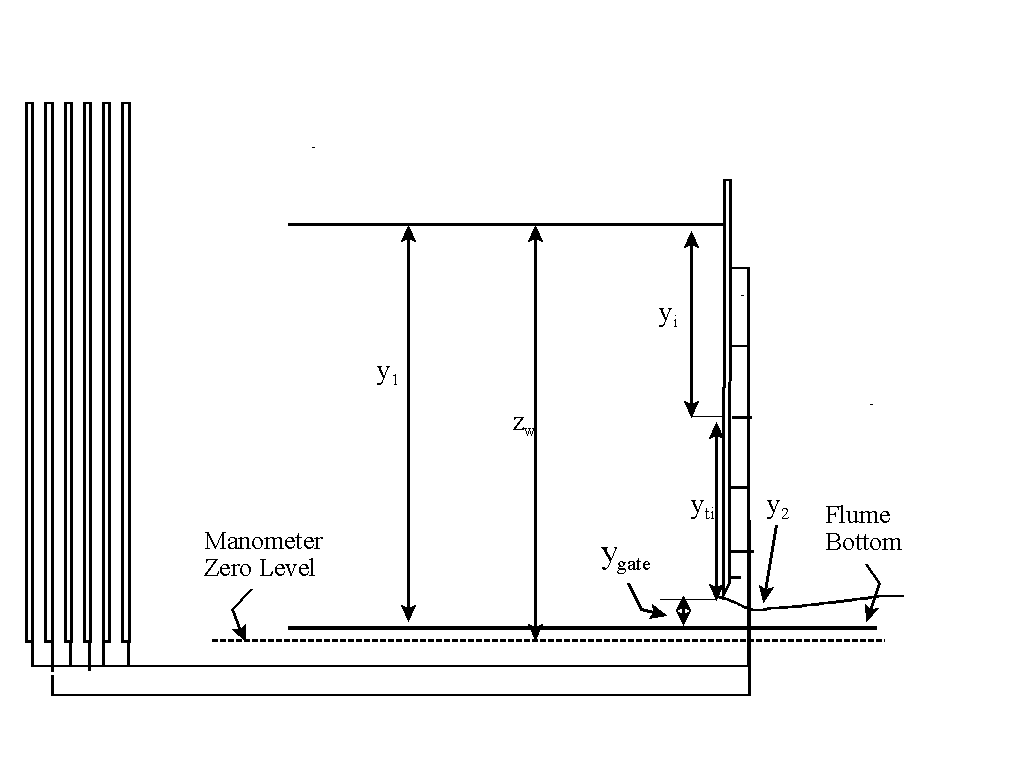
Note: Manometer (pressure) taps show the water pressure on the other side of the sluice gate in the center of the channel

Force By Momentum Equation

F_x = γ* V_x *Q      becomes
F_g = γ*[Q*(V₁ -V₂) + 0.5*b* (y₁²-y₂²)]

where γ = density of water
       g (in the drawing) = gravity constant
       Q = flow rate
       v₁, y₁ = upstream velocity and depth
       v₂, y₂ = downstream velocity and depth
       b = width of rectangular channel





Force By Hydrostatic Model & By Direct Measurement


Linear hydrostatic pressure uses the simple triangular pattern of pressure, with the average pressure at the center point times the area. (In our experiment, the top pressure is atmospheric, which we use as H₁ of zero.)

Direct measurement uses pressure measured at several points along the gate. The key is to select the area you associate with each pressure value.

SLUICE GATE EXPERIMENT: PREPARATION

OBJECTIVES (Presented above)

APPARATUS (Same flume & measurement taps as for Weir Experiment, except tap on the sluice gate)

SET UP EXPERIMENT:
Open surge tank valve. Open both the head and the tail (sluice) gates of the half-meter open channel unit

Determine the longitudinal profile along the centerline of the floor of the flume to get point gage zeros. (If not clear from a prior experiment.)

Remove air from all manometric tubing. Locate the pressure taps in the gate and on the floor of the flume and match them to the manometer columns.

Close the drain valve, start the large pump, and open the intake valve.

Measure the profile and the sluice gate variables.
Establish a steady flow in the flume

Lower the upstream sluice gate until it impinges on the flow.

Slowly lower the gate until the flume is nearly full.
   Wait for the flow to reach the steady state.
   [Note: remove air from the manometer tubes A-F.]

Record the flow depths of the water surfaces both upstream and downstream of the gate. For the supercritical section, you are trying to measure at the vena contracta.

Repeat step d until you have at least 6 measurements of depth


Measure the water surface profile & taps A-F
Cloes the sluice gate enough to raise level above taps A-F

Measure the depth of the water to about half-way down the channel

Also record the levels at taps A-F

Sluice Gate in Our Flume

SLUICE GATE EXPERIMENT: RESULTS

Attach your data sheet and sketch of the experimental set-up

Flow Through Sluice Gate
Using the continuity equation between the upstream and downstream flows (latter at the vena contracta) compute the velocities on both sides of the gate for each pair of flow depths.
From Q = V_iA_i
    V₁ = Q/(b*y₁) and V₂ = Q/(b*y₂)

Compare the specific energy (E_i = y_i + V_i² /2g) plot for the observed depths and computed velocities with the theoretical plot at the same flow rate, Q

Compare the measured contraction coefficient with any hydraulic literature reference.



Flow Rate Calculation
Using your depth measurements upstream of the gate and at the vena contracta, along with the continuity and energy equations, compute the flow rate and compare it with the rate given by the flow meter
Q = V₁*A₁ = V₂*A₂
E_i = y_i + V_i² /2g
or      y₁ + V₁² /2g = y₂ + V₂² /2g

Combining these:     Q = 2g*b* y₁* y₂ / (y₁ + y₂)^0.5

Force On Gate
Compute the force on the gate using (a) the measured pressures, (b) hydrostatic assumption, and (c) the momentum equation.
Compare the three values in terms of accuracy and convenience.


Plot the pressure distributions on the upstream side of the sluice gate from the measured pressures and from the hydrostatic assumption on the same chart and compare the two patterns.

Roberson, John, & Clayton Crowe, ENGINEERING FLUID MECHANICS, 4th Ed., Houghton Mifflin Co., 1990. Ch. 6 & 15